|
ELEMENTS DE CALCUL POUR LA
CONTRUCTION DES ETANGS :
APPROCHE DU VOLUME DE TERRE D’UNE DIGUE
Un gros problème du travail avec les
tâcherons est que le prix des contrats est d’abord estimé sur la
longueur de la digue et/ou la surface de l’étang de service. Ces
critères ne sont pas très bons car une digue peut être plus ou moins
large, plus ou moins haute ; un étang de service assez grand peut,
par exemple, demander moins de travail qu’un petit étang si son
emplacement a été judicieusement choisi et si le site s’y prête.
L’un des indicateurs pour estimer le
travail réalisé sur lequel il est intéressant de réfléchir est le
volume de terre déplacé : c’est à dire quelle est la quantité
de terre qu’il a fallu mettre sur la digue. Comment mesure-t-on une
quantité de terre ? En faisant une estimation du volume de terre. On
peut mesurer le volume en bassine, en brouette ou en m3. C’est
cette dernière unité que nous utiliserons ici (1 m3
correspond à 1000 litres soit près de 50 cuvettes et à peu près 20
brouettes). La quantité de terre paraît juste pour estimer la quantité
de travail pour construire la digue.
Deux autres éléments ne seront pas
traités ici, ils influencent la quantité de travail, il s’agit :
- De la distance sur laquelle il va falloir transporter
cette terre ?
- Et, quel est le travail qu’il faudra fournir pour creuser la
terre ?

Schéma a : digue idéale sur
une vallée avec
deux versants parfaitement plats
Comme souvent, il est très difficile
dans les conditions d’un chantier au village de mesurer exactement la
quantité de terre. Le terrain n’est pas régulier, les appareils pour
le mesurer (la lunette topographique, en particulier) doivent être
manipulés de nombreuses fois pour avoir des données assez précises.
Nous vous proposons ci-après deux
méthodes d’estimation des quantités de terre à creuser.
Ce sont des méthodes simplifiées, c’est à dire qu’elles ne
recherchent pas à être exactes mais à donner la meilleure idée
possible du volume des digues par un calcul " assez "
simple.
Première méthode : C’est la
plus simple.
On assimile la digue à une digue parfaitement régulière qui serait
construite sur une vallée dont les deux versants seraient deux plans
parfaitement réguliers (ce cas de figure n’existe jamais dans la
réalité). D’où le schéma a suivant :
ld : largeur de la banquette
(largeur du haut de la digue)
hm : hauteur maximale
e : la digue (au niveau de la vidange)
L : longueur de la digue d’un côté à l’autre du bas-fond
Toutes ces distances doivent être exprimées en mètres.
Le volume de cette digue en mètre cube
est :
|
V digue = L/2 x hm x [ 0,77 x hm
+ ld] |
Deuxième méthode :
La deuxième méthode proposée sera
détaillée dans le prochain numéro, elle est plus compliquée que la
première.

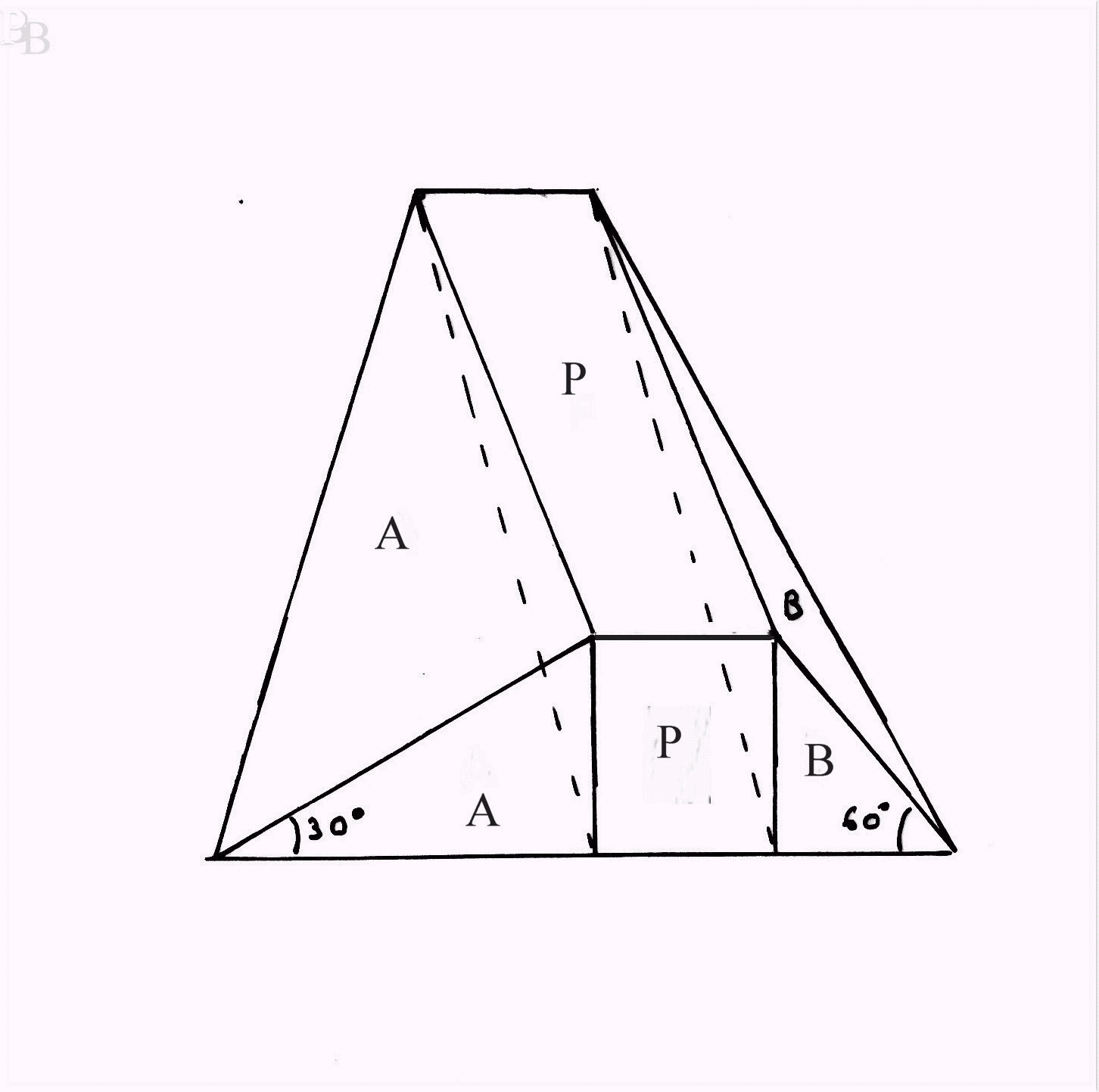
Schéma B : une demi
digue est composée
de deux pyramides et d’un demi
parallélépipède.
Pour les forts en math, comment
obtient-on cette formule
Premièrement, on coupe la digue en
deux, par le milieu, le long de la digue, pour faire deux parties égales.
Si on regarde maintenant une moitié de
la digue, on s’aperçoit que ce volume se découpe en trois formes
géométriques simples : deux pyramides (A et B) et une moitié de
parallélépipède.
Rappelons que le volume d’une pyramide
est 1/3 multiplié par la surface de la base multipliée par la hauteur de
celle-ci, le volume d’un parallélépipède est égal au produit de sa
longueur par sa largeur par sa hauteur.
Pour la pyramide A, celle à l’intérieur
de l’étang.
La hauteur de la pyramide est la longueur de la digue divisée par deux,
soit L/2.
La surface de la base est la hauteur maximale de la digue multipliée par
la longueur de la pente intérieure et divisée par deux. Or la longueur
de la pente au sol est à peu près égale à 1,7 x la hauteur de la
digue, soit :
Surface base = ½ x hm x 1,7 hm
Donc pour la pyramide qui se tourne vers
l’étang, son volume V1 est :
VA = 1/3 x L/2 x ½ x hm x 1,7 hm
Pour la pyramide B, celle à l’extérieur
de l’étang.
La hauteur de la pyramide est la même que pour la A, c’est la longueur
de la digue divisée par deux soit L/2.
La surface de la base est la hauteur
maximale de la digue multipliée par la longueur de la pente extérieure
et divisée par deux. Or la longueur de la pente est
égale à peu près à 0,6 x la hauteur
de la digue, soit :
Surface base = ½ x hm x 0,6 hm
Donc pour la pyramide à l’extérieur
de l’étang, son volume V2 est :
VB = 1/3 x L/2 x ½ x hm x 0,6 x hm
Pour la moitié du parallélépipède,
le volume est égal à la longueur de celui-ci, L/2, multiplié par sa
hauteur, hm, multiplié par sa largeur l, le tout divisé par deux :
Soit
Vp = ½ x L/2 x ( hm x ld)
Le volume total de la demi - digue est
donc égal à la somme des trois volumes
V demi-digue = VA + VB + Vp
Le volume total de la digue est le
double de celui de la demi-digue, il est donc :
V digue = 2 x V demi-digue
V digue = 2 x VA + 2 x VB + 2 x Vp
Ce qui donne, après
simplification : V digue = L/2 x
hm x [ (1,7 + 0,6)/3 x hm + ld]
Soit à peu près :
V digue = L/2 x hm x [ 0,77 x hm + l]
Exercice pour les volontaires, vous avez
6 mois pour faire parvenir votre réponse au journal.
Une digue fait 2,5 m de hauteur au niveau du moine et 45 m de long, la
banquette fait 2, 5 m de large, quel est son volume ?
Marc OSWALD
|
Recevez tous nos Vœux
de Bonne Année 2003
Bon courage à tous
La rédaction |
|

